Asymmetric Encryption
Asymmetric cryptography is in many ways completely different than symmetric cryptography. While both are used to keep data from being seen by unauthorized users, asymmetric cryptography uses two keys instead of one. It was invented by Whitfield Diffie and Martin Hellman in 1975. Asymmetric cryptography is more commonly known public key cryptography. The system uses a pair of keys: a private key that is kept secret and a public key that can be sent to anyone. The system's security relies upon resistance to deducing one key, given the other, and thus retrieving the plaintext from the ciphertext.
RSA
RSA is one of the first public key cryptosystems ever invented. It can be used for both encryption and digital signatures. RSA is named after its inventors, Ron Rivest, Adi Shamir, and Leonard Adleman, and was first published in 1977. This algorithm uses the product of two very large prime numbers and works on the principle of difficulty in factoring such large numbers. It's best to choose large prime numbers from 100 to 200 digits in length and that are equal in length. These two primes will be P and Q. Randomly choose an encryption key, E, so that E is greater than 1, E is less than P * Q, and E must be odd. E must also be relatively prime to (P - 1) and (Q - 1). Then compute the decryption key D:
D = E-1 mod ((P - 1)(Q - 1))
Now that the encryption key and decryption key have been generated, the two prime numbers can be discarded, but they should not be revealed. To encrypt a message, it should be divided into blocks less than the product of P and Q. Then,
Ci = Mi E mod (P * Q)
C is the output block of ciphertext matching the block length of the input message, M. To decrypt a message take ciphertext, C, and use this function:
Mi = Ci D mod (P * Q)
The use of the second key retrieves the plaintext of the message.
This is a simple function, but its security has withstood the test of more than 20 years of analysis. Considering the effectiveness of RSA's security and the ability to have two keys, why are symmetric encryption algorithms needed at all? The answer is speed. RSA in software can be 100 times slower than DES, and in hardware it can be even slower.
Diffie-Hellman
Diffie-Hellman was created in 1976 by Whitfield Diffie and Martin Hellman. This protocol is one of the most common encryption protocols in use today. It plays a role in the electronic key exchange method of the Secure Sockets Layer (SSL) protocol. It is also used by the SSH and IPsec protocols. Diffie-Hellman is important because it enables the sharing of a secret key between two people who have not contacted each other before.
The protocol, like RSA, uses large prime numbers to work. Two users agree to two numbers, P and G, with P being a sufficiently large prime number and G being the generator. Both users pick a secret number, a and b. Then both users compute their public number:
User 1 X = Ga mod P, with X being the public number User 2 Y = Gb mod P, with Y being the public number The users then exchange public numbers. User 1 knows P, G, a, X, and Y.
User 1 Computes Ka = Ya mod P User 2 Computes Kb = Xb mod P
With Ka = Kb = K, now both users know the new shared secret K. This is the basic algorithm, and although there have been methods created to strengthen it, Diffie-Hellman is still in wide use. It remains very effective because of the nature of what it is protecting-a temporary, automatically generated secret key that is good only for a single communication session.
ElGamal
ElGamal can be used for both encryption and digital signatures. Taher ElGamal designed the system in the early 1980s. This system was never patented and is free for use. It is used as the U.S. government standard for digital signatures.
The system is based upon the difficulty of calculating discrete logarithms in a finite field. Three numbers are needed to generate a key pair. User 1 chooses a prime, P, and two random numbers, F and D. F and D should both be less than P.
ECC
Elliptic curve cryptography (ECC) works on the basis of elliptic curves. An elliptic curve is a simple function that is drawn as a gently looping curve on the X,Y plane. They are defined by this equation:
y2 = x3 + ax2 + b
Elliptic curves work because they have a special property-you can add two points on the curve together and get a third point on the curve. For cryptography, the elliptic curve works as a public key algorithm. Users agree on an elliptic curve and a fixed curve point. This information is not a shared secret, and these points can be made public without compromising the security of the system. User 1 then chooses a secret random number, K1, and computes a public key based upon a point on the curve:
P1 = K1 * F
User 2 performs the same function and generates P2. Now user 1 can send user 2 a message
by generating a shared secret:
S = K1 * P2
User 2 can generate the same shared secret independently:
S = K2 * P1 This is true because
K1 * P2 = K1 * (K2 * F) = (K1 * K2) * F = K2 * (K1 * F) = K2 * P1
The security of elliptic curve systems has been questioned, mostly because of lack of analysis. However, all public key systems rely on the difficulty of certain math problems.
It would take a breakthrough in math for any of the mentioned systems to be weakened dramatically, but research has been done about the problems and has shown that the elliptic curve problem has been more resistant to incremental advances. Again, as with all cryptography algorithms, only time will tell how secure they really are.
Asymmetric Encryption Summary
Asymmetric encryption creates the possibility of digital signatures and also corrects the main weakness of symmetric cryptography. The ability to send messages securely without senders and receivers having had prior contact has become one of the basic concerns with secure communication. Digital signatures will enable faster and more efficient exchange of all kinds of documents, including legal documents. With strong algorithms and good key lengths, security can be assured.
Steganography
Steganography, an offshoot of cryptography technology, gets its meaning from the Greek steganos meaning covered. Invisible ink placed on a document hidden by innocuous text is an example of a steganographic message. Another example is a tattoo placed on the top of a person's head, visible only when the person's hair is shaved off. Hidden writing in the computer age relies on a program to hide data inside other data. The most common application is the concealing of a text message in a picture file. The Internet contains multiple billions of image files, allowing a hidden message to be located almost anywhere without being discovered. The nature of the image files also make a hidden message difficult to detect. While it is most common to hide messages inside images, they can also be hidden in video and audio files.
Steganographic encoding can be used in many ways and through many different media. Covering them all is beyond the scope for this short study guide, but we will discuss one of the most common ways to encode into an image file, LSB encoding. LSB, Least Significant Bit, is a method of encoding information into an image while altering the actual visual image as little as possible. A computer image is made up of thousands or millions of pixels, all defined by 1s and 0s. If an image is composed of Red Green Blue (RGB) values, each pixel has an RGB value represented numerically from 0 to 255. For example, 0,0,0 is black, and 255,255,255 is white, which can also be represented as 00000000, 00000000, 00000000 for black and 11111111, 11111111, 11111111 for white. Given a white pixel, editing the least significant bit of the pixel to 11111110, 11111110, 11111110 changes the color. The change in color is undetectable to the human eye, but in a image with a million pixels, this creates a 125KB area in which to store a message.
Cryptography Algorithm Use
liqjJr, lOOlQllQOUllQlQlQOOlOlOOOm lr^MjllOlOOlOlOlOlOl 1G00011101010U)
^Ш 1010011010010101101010001001
JM 010101010101010100001101011 010010011101001101010001100 ib lioiioiiiioooiioioioioonoii
oiooiu. -Jiooiooiiioioioioiioooioiii looooioioiiooiooioioioioioioom loioi 0101010000101001011101010111101000110 0110101010101001011101010100010011110 1001010100100011011010110101010011011 0100101001010010011101010101100010101 1000010101100100101010101010011110010
The use of cryptographic algorithms grows every day. More and more information becomes digitally encoded and placed online, and all of this data needs to be secured. The best way to do that with current technology is to use encryption. Security is typically defined as a product of five components:
ting and certification tools, WWW, testkina. com confidentiality, integrity, availability, authentication, and nonrepudiation. Encryption addresses four of these five components: confidentiality, integrity, nonrepudiation, and authentication.
Confidentiality
Confidentiality typically comes to mind when the term security is brought up. Confidentiality is the ability to keep some piece of data a secret. In the digital world, encryption excels at providing confidentiality. Confidentiality is used on stored data and on transmitted data. In both cases, symmetric encryption is favored because of its speed and because some asymmetric algorithms can significantly increase the size of the object being encrypted. In the case of a stored item, a public key is typically unnecessary, as the item is being encrypted to protect it from access by others. In the case of transmitted data, public key cryptography is typically used to exchange the secret key, and then symmetric cryptography is used to ensure the confidentiality of the data being sent.
Asymmetric cryptography does protect confidentiality, but its size and speed make it more efficient at protecting the confidentiality of small units for tasks such as electronic key exchange. In all cases, the strength of the algorithms and the length of the keys ensure the secrecy of the data in question.
Integrity
Integrity is better known as message integrity, and it is a crucial component of message security. When a message is sent, both the sender and recipient need to know that the message was not altered in transmission. This is especially important for legal contracts- recipients need to know that the contracts have not been altered. Signers also need a way to validate that a contract they sign will not be altered in the future. Integrity is provided with one-way hash functions and digital signatures. The hash functions compute the message digests, and this guarantees the integrity of the message by allowing easy testing to determine whether any part of the message has been changed.
The message now has a computed function (the hash value) to tell the users to resend the message if it was intercepted and interfered with.
Nonrepudiation
An item of some confusion, the concept of nonrepudiation is actually fairly simple. Nonrepudiation means that the message sender cannot later deny that she sent the message. This is important in electronic exchanges of data, because of the lack of faceto-face meetings. Nonrepudiation is based upon public key cryptography and the principle of only you knowing your private key. The presence of a message signed by you, using your private key, which nobody else should know, is an example of nonrepudiation.
When a third party can check your signature using your public key, that disproves any claim that you were not the one who actually sent the message. Nonrepudiation is tied to asymmetric cryptography and cannot be implemented with symmetric algorithms.
Authentication
Authentication lets you prove you are who you say you are. Authentication is similar to nonrepudiation, except that authentication often occurs as communication begins, not after. Authentication is also typically used in both directions as part of a protocol. Authentication can be accomplished in a multitude of ways, the most basic being the use of a simple password. Every time you sign in to check your e-mail, you authenticate yourself to the server. This process can grow to need two or three identifying factors, such as a password, a token (such as a digital certificate), and a biometric (such as a fingerprint).
Digital Signatures
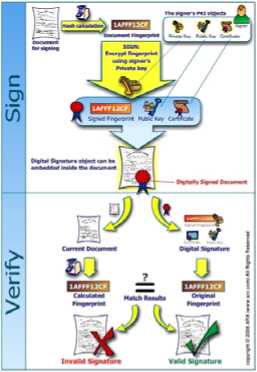
Digital signatures have been touted as the key to truly paperless document flow, and they do have promise for improving the system. Digital signatures are based on both hashing functions and asymmetric cryptography. Both encryption methods play an important role in signing digital documents.
Unprotected digital documents are very easy for anyone to change. If a document is edited after an individual signs it, it is important that any modification can be detected. To protect against document editing, hashing functions are used to create a digest of the message that is unique and easily reproducible by both parties. This ensures that the message integrity is complete.
Key Escrow
The impressive growth of the use of encryption technology has led to new methods for handling keys. Encryption is adept at hiding secrets, and with computer technology being affordable to everyone, criminals and other ill-willed people began using it to conceal communications and business dealings from law enforcement agencies. Because they could not break the encryption, government agencies began asking for key escrow. Key escrow is a system by which your private key is kept both by you and by the government. This allows people with a court order to retrieve your private key to gain access to anything encrypted with your public key. The data is essentially encrypted by your key and the government key, giving the government access to your plaintext data.
